GRAPH THEORY,ITS OMNIPRESENCE AND AN APPLICATION IN COMPUTER SECURITY

The rapid pace at which technology is growing is based on the presence
of an omnipresent factor-- Graph theory. Graph theory has been and is the
integral part of our lives. Normally, we do not observe the importance of
graph theory, but if we do, carefully, then the whole world is nothing but a
huge network. Right from people communicating from various parts of the
world to the constellations, brain mapping, neural networks, and what not?!!!
Graph theory has its own role to play. Graph theory is one such subject which
has deep rooted its existence in the field of computer security and not to
forget it has its role in most of the field’s today.
Amidst this growth, lets us pause and think for a minute—how do we feel
so secure while transacting on the INTERNET where we need to use ID's,
passwords and so on.....

Let us consider a hypothetical situation and try to learn many beautiful yet
very, very astonishing concepts in Graph theory. Along the way through this
example we shall learn many new concepts without our knowledge!!! Such is
the simplicity of this beautiful subject.

Imagine yourself to be in a situation like the one which follows:

Consider a bank, secondly the bank has an astonishingly intelligent guard,
finally but obvious the bank has a very huge client base and you are an
esteemed customer and an intelligent computer scientist.
The security guard has no aid what so ever to learn the customer's
authenticity. Each customer is given an unique id and the password is left to
choose by him/her(as of now we believe in supporting these two cases only!! ).

Since the user id is key to address/ recognize, but now how exactly the
security can come to know that the person having the id is the exact person
himself?

Since photo or etc isn’t available(the case is hypothetical), mentioning the
password is the only option.
So person who can tell the password is supposedly to be the authenticated
person!

Now, you come to the bank, security guard will stop you and ask you for your
id. Your id can be known by any one (it just requires one's smartness). So the
security asks you for your password. Now if you reveal your password ,the
whole idea of security through a password is blown away!!

Look here lies the problem :
you need to enter the bank, but to do that you need to convince the
security guard by authenticating yourself by telling him the password (which
is the only way out—remember??).
How can this be done?
Now here is a tricky solution.
In cryptography(a branch of graph theory), a zero-knowledge proof or zero
knowledge protocol is the solution. This is an effective method where in one
can prove to the other that his statement is true(by mathematics) without
revealing anything other than the truthfulness of the statement.
For zero-knowledge proof, graph theory provides an easy way by the vertex
coloring method. It is an assignment of labels traditionally called "colors" to
elements of a graph subject to certain conditions. In its simplest form, it is
a way of coloring the vertices of a graph such that no two adjacent vertices
share the same color; this is called a vertex coloring. The smallest number of
colors needed to color a graph by satisfying the above condition is called its
chromatic number.

Now for a graph having few vertices and arranged well, it’s easy to fill color
for the said criteria.
(pic)
So, here basically the pattern of edges we choose to connect them between
two vertices represents the password. Since set of vertices can be connected
in various ways, the way in which we select the number of vertices and
edges linking mechanism will form the foundation for you to create the
password. Once you are done “developing” your password, it will result in
a very complex graph which will be very difficult to decode. If the customer
is asked to reveal his password, then he has to displace the nodes of the
graph in a random fashion, but care has to be taken that no edges are broken down.



Now you show the graph ,by covering all the vertices and ask the security to
choose ,you tell him that you have filled in proper coloring, so that none of the
vertices sharing edges have the same color ( none but u can solve it easily,
method illustrated later)

The security now starts choosing , after several tries he may feel that
each time by mere coincidence or luck you have filled them correctly.
Mathematically the probability that security always lifts the correctly filled

edge is only ½. Owing to this fact there were equal chances of picking up
the wrong ones. This clearly convinces him that you have filled the colors to
the vertices perfectly.

Next question is--- What if this security sits and starts decoding and finally
figures out the correct password and turns rich?

This is practically impossible .Since this solution is an one way function, i.e.,
a function that is easy to compute, but nevertheless, it is difficult to compute
its inverse. In simple words, it means it’s easy to verify the solution but
extremely difficult to solve.

Consider a simple example of a one-way function which we do day-in and
day-out.

TYPING is actually a one-way-function.

Position your fingers on the keyboard in the natural position for typing "asdf
jkl;". Press the "Y" key on your keyboard without looking at the keyboard.
Very easy to do. Our brains are programmed to do this quickly what we call it
the learnt reflexes!

Now take your hands off of the keyboard. Point your right middle-finger down.
If your hands were on the keyboard, which key would you be pressing? Now
point your right pinky up. If you hands were on the keyboard, which key would
you be pressing? Much harder to do.

It is called the P Vs NP problem.

Another simple example is given below.
Say you are looking for a person with certain qualities such as fair,
handsome, intelligent, six-pack abs, IQ level > 140. This is an hypothetical
case, but if found its very easy to verify if he satisfies these criteria.

Now coming to the graph. Look at the graph below. As and when the vertices
and corresponding edges grow complexity increases to such an extent that it
is impossible to decode but can easily be verified.



The fig.2.(left pic) is just obtained by shuffling the vertices and their respective edges present in fig.3.(bottom-right pic)


By this way, the customer will ensure that his privacy is not curbed. If in
case, the guard is not yet satisfied with the customer, the graph is arranged
haphazardly and the above process is repeated. So by this, the guard, at
some point, will be satisfied( and exhausted!) by the customers identity.

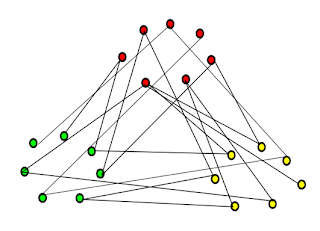
Filling colors:(Technique now explained as to how we can do it easily, i.e.,
code our password)
Take three circles representing 3 colors , fill in the vertices to them to exhaust
all. Make complex pattern of your choice ,but not by connecting the vertices
present in the circle it self. Now pull aside the vertices in these circles to a
complex patter ensuring that no edges are broken. IT WILL RESULT IN A
COMPLEX GRAPH WHICH CANNOT BE DECODED EVEN AFTER DAYS
OF HARD WORK.

The graph show below is clear example of an one way function.
The three colouring process is easy to do one way but not the vice-versa
i.e .,it is easy to verify that if the edges have fulfilled the criteria but its
extremely difficult to colour the vertices to the said criteria.

COMBINATIONS

"Nature is an endless combination and repetition of a very few laws. She hums the old well-known air through innumerable variations"

~ Ralph Waldo Emerson (American Poet, Lecturer and Essayist, 1803-1882)

Every living being is a combination of various cells. Every inanimate object around us is a combination of atoms. Every machine is a combination of various individual parts. For example, your car has the gear shaft, brakes, accelerator, engine, steering wheel etc…..What matters most to you is that the car has all these essential parts rather than the internal arrangement of these parts. Or consider treating your friends on your birthday. All that is important is that which of your friends come, not the order in which they sit around the table. Thus all your friends constitute a selection where the order is completely unimportant. Such a selection is called a COMBINATION.

Consider another scenario. Suppose you are at a candy shop that has say 20 types of chocolates. You decide to buy 5 chocolates, each of a different type. Here choosing 5 different chocolates is important than the order in which you pick them. By rule of product, there are

20*19*18*17*16=$\frac{20!}{15!}$= P(20,5)

possibilities of choosing 5 chocolates from 20 in succession and without replacement. Since the order in which chocolates are chosen is not important, we remove 5!(corresponding to permutations of 5 chocolates). Therefore :

$\frac{20!}{5!15!}$= 15504 ways!!

The number of ways in which you can choose 5 chocolates out of 20 is called C(20,5), read as 20choose 5 and is equal to 15504.

More generally, the number of ways in which r objects from n distinct objects , with no reference to order is given by

C(n,r)=$\frac{P(n,r)}{ r!}$ = $\frac{n!}{ r!(n-r)!)}$ 0≤r≤n.

Further,

For all n≥0 , C(n,0)=C(n,n)=1.

For n≥1, C(n,1)=C(n,n-1)=n

When 0≤n≤r, then C(n,r)=0

COMBINATIONS WITH REPETITIONS

In the previous example of picking chocolates, we picked 5 different chocolates that is to say no two chocolates chosen were identical. Or in other words, repetition wasn’t allowed. If we were to say that you could pick more than one chocolate of a given type then it becomes a more intriguing problem. This brings us to a concept called Combinations with repetitions, meaning, the number of combinations of n objects taken r at a time, with repetition. The following example illustrates this concept.

Let us say there are five flavors of ice cream: banana, chocolate, lemon, strawberry and vanilla. You can have three scoops. How many variations could there be? Let's use letters for the flavors: {b, c, l, s, v}. Example selections would be {c, c, c} (3 scoops of chocolate) {b, l, v} (one each of banana, lemon and vanilla) {b, v, v} (one of banana, two of vanilla)

(And just to be clear: There are n=5 things to choose from, and you choose r=3 of them.
Order does not matter, and you can repeat!)

Here’s a special technique that lets you work it out.

	Think about the ice cream being in containers, you could say "skip the first, then 3 scoops, then skip the next 3 containers" and you will end up with 3 scoops of chocolate!
	So, it is like you are ordering a robot to get your ice cream, but it doesn't change anything, you still get what you want.

Now you could write this down as (arrow means skip, circle means scoop)

In fact the three examples above would be written like this:

{c, c, c} (3 scoops of chocolate):
{b, l, v} (one each of banana, lemon and vanilla):
{b, v, v} (one of banana, two of vanilla):

OK, so instead of worrying about different flavors, we have a simpler problem to solve: "how many different ways can you arrange arrows and circles"

Notice that there are always 3 circles (3 scoops of ice cream) and 4 arrows (you need to move 4 times to go from the 1st to 5th container).

So (being general here) there are r + (n-1) positions, and we want to choose r of them to have circles.

This is like saying "we have r + (n-1) pool balls and want to choose r of them". In other words it is now like the pool balls problem, but with slightly changed numbers. And you would write it like this:

where n is the number of things to choose from, and you choose r of them (Repetition allowed, order doesn't matter)

Interestingly, we could have looked at the arrows instead of the circles, and we would have then been saying "we have r + (n-1) positions and want to choose (n-1) of them to have arrows", and the answer would be the same ...

This brings us to a formula derived by a celebrated mathematician Leonhard Euler(1707-1783).

So, what about our example, what is the answer?

(5+3-1)!	=	7!	=	5040	= 35
3!(5-1)!		3!×4!		6×24

Euler’s derivation of the formula for combinations with repetitions:

Suppose we have n distinct objects. We can label them with the integers from 1 to n. Now consider a k-combination, that is, an unordered selection of k integers, possibly with repetitions, from among 1....n, say i₁, i₂, ..., i_k. Even though we do not care about the order, we can certainly arrange the selected integers in order, for convenience in counting the possibilities. Suppose therefore that the sequence i₁, i₂, ..., i_k is in increasing order (but not strictly). Then the sequence

i₁, i₂+1, i₃+2, ..., i_k+(k-1)

is a strictly increasing sequence of k integers selected from the integers from 1 to n+k-1. Moreover each such sequence can occur. The number of such sequences is the number of k-combinations, without repetition, from n+k-1 distinct objects. Thus the number of k-combinations, with repetitions, from n distinct object is

Here is another way to view k-combinations: suppose we have n distinct cells (boxes) and k indistinguishable objects (think of x's) to place in the cells. How many ways can it be done? Order the cells, so we can refer to them by number. Lay out the objects (the x's) in a line. Place dividers between them to divide them into lots that go in successive cells. We will require n-1 dividers. A configuration of objects and dividers looks like

xxx|xx|xxxx|||xx|xxx

Here 3 x's go in the first cell, 2 x's in the second, 4 x's in the third, none in the fourth, and so on. Each such configuration is completely determined by the location of the dividers. Thus we must choose n-1 locations out of a total of n+k-1 locations for the dividers. This can be done in C(n+k-1,n-1)= C(n+k-1,k) ways.

Now the configuration above can also be described without the dividers simply by labelling each x according to the cell it goes in, for example by using successive letters of the alphabet. Thus the configuration above could be described by

aaabbccccffgg

We see immediately that C(n+k-1,n-1)= C(n+k-1,k) is equal to the number of possibly distinct partial derivatives of total order k for a function of n variables.

Alternatively you could adopt a whole new approach to solve such problems. If you are allergic to the use of formulae , then the following method could work wonders for you-

Suppose that you want to choose, with repetition and disregarding order, n objects of k distinct types. You can encode each selection as a binary sequence like this:

- Take k - 1 0's and n 1's; the 0's function as markers to separate the distinct kinds of objects, while the 1's represent the selected objects.

- The sequence has the form 1...101...101.....1.
To give an example, suppose that you have three objects, {a,b,c} and choose 5 of them each time; then typical selections will look like (disregarding order):

aabcc, abbbc, bbccc, aaacc, etc.

And the corresponding sequences are: 1101011, 1011101, 0110111, 1110011

Note that you need only two 0's to distinguish three kinds, and that the sequences begins, ends, or have consecutive 0's if at least one of the kinds is not selected.

But then you reduced the original problem to the one of counting a particular class of binary sequences which is typically much easier: the sequences will have length n + k - 1, and k - 1 0's; as C(m,j) counts the number of length m sequences with j 1's, then you have C(n + k - 1,n). There, that’s not so difficult isn’t it?

How many ways can I select 15 cans of soda from a cooler containing large quantities of Coke,

Pepsi, Diet Coke, Root Beer and Sprite?

• We have to model this problem using the chart:

Coke Pepsi Diet Coke Root Beer Sprite

A: 111 111 111 111 111 =15

B: 11 111111 111111 1 =15

C: 1111 1111111 1111 =15

• Here, we set an order of the categories and just count how many from each category are chosen.

• Now, each event will contain fifteen 1’s, but we need to indicate where we transition from one

Category to the next. If we use 0 to mark our transitions, then the events become:

A: 1110111011101110111

B: 1100111111011111101

C: 0011110111111101111

• Thus, associated with each event is a binary string with #1’s = #things to be chosen and #0’s =

#transitions between categories.

• From this example we see that the number of ways to select 15 sodas from a collection of 5 types of

soda is C(15 + 4,15) = C(19,15) = C(19,4).

• Note that #zeros = #transitions = #categories -1.

• Theorem: The number of ways to fill r slots from n

categories with repetition allowed is:

C(r + n-1, r) = C(r + n -1, n -1).

• In words, the counts are:

C(#slots + #transitions, #slots)

The number of combinations of three letters a,b,c arranged two at a time is:

$\frac{(3+2-1)!}{2!(3-1)!}$ =6

a,a /a,b / a,c / b,b / b,c/ c,c

Problems involving combinations with repetitions can also be solved using a table like the one that follows:

Here n= no of distinct objects and r is the no. of objects selected at a time.

The concept of combinations with repetitions can be used not only to find the number of ways a selection can be made in real life situations, but also to determine the time-efficiency of various algorithms. Thus it is an extremely useful concept in discrete mathematics.

By.

Deepthi P Hudedagaddi and

(deepthiph@gmail.com)

Pallavi Ravishankar

(pallavi23ravi@gmail.com)

article on combinations with repetitions

This is the link for the article on combinations with repetetions(by pallavi and deepthi)

https://docs.google.com/document/d/1kBrPQB7UxiIgzc1PjFRQzxa0ug-d_GdTujRqmZ7BtCo/edit?hl=en&pli=1&authkey=CJGFjaYK#


The article will be posted here shortly....

fact

$\frac{20!}{15!}$

Pallavi's test

$\int_{a}^{b}sinx$


$\begin{pmatrix} n\\ 2 \end{pmatrix}$

This is how we type math equations.



$\alpha$

New Test post

$\frac{a}{b}$

Test post

$(a+b)^2= a^2 + b^2 + 2ab$

testing whether math typesetting works fine!